Rings of Callicrates
Last Updated: September 12, 2002
Up
Clifford Pickover described a variety of magic circles,
including one he called Rings of Callicrates (Figure 4.24 in
Pickover's book). The original
ring (created by Michael Keith) has the digits of pi on the outer
node points:
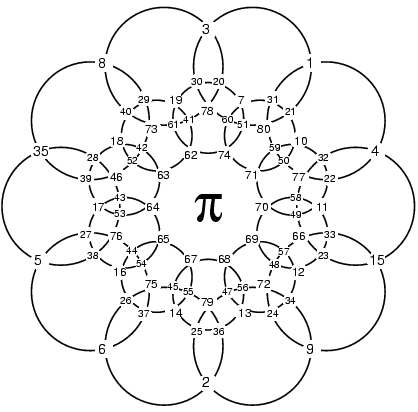
This type of ring structure falls into the type I call
simple, and other orderings of
the numbers are possible:
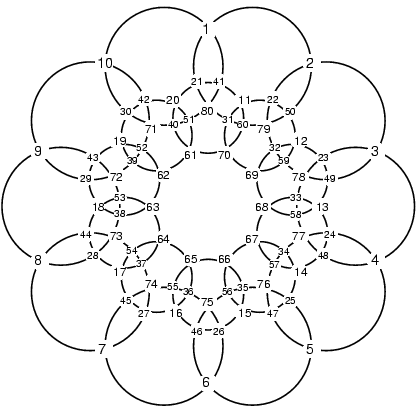
The above two sets of circles have two rings of 10 circles each.
There is nothing special about having 10 circles; rings with
more or less circles are easily constructed. Here are examples
with 12 and 15 circles:
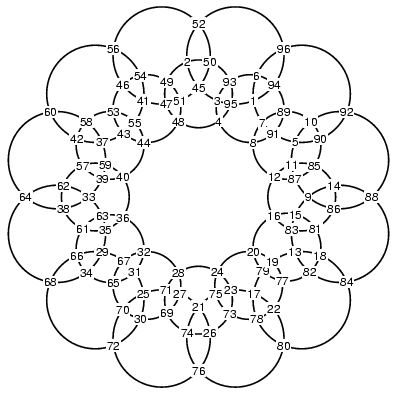
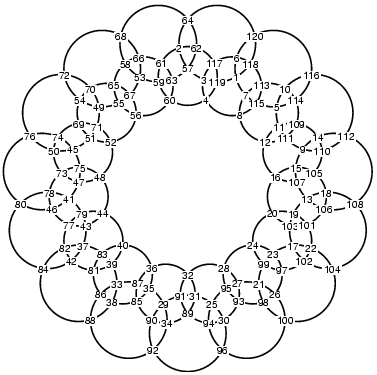
Further, we can add additional layers of rings, although we must
be careful with the connectivity to ensure that each ring has
the same number of intersections:
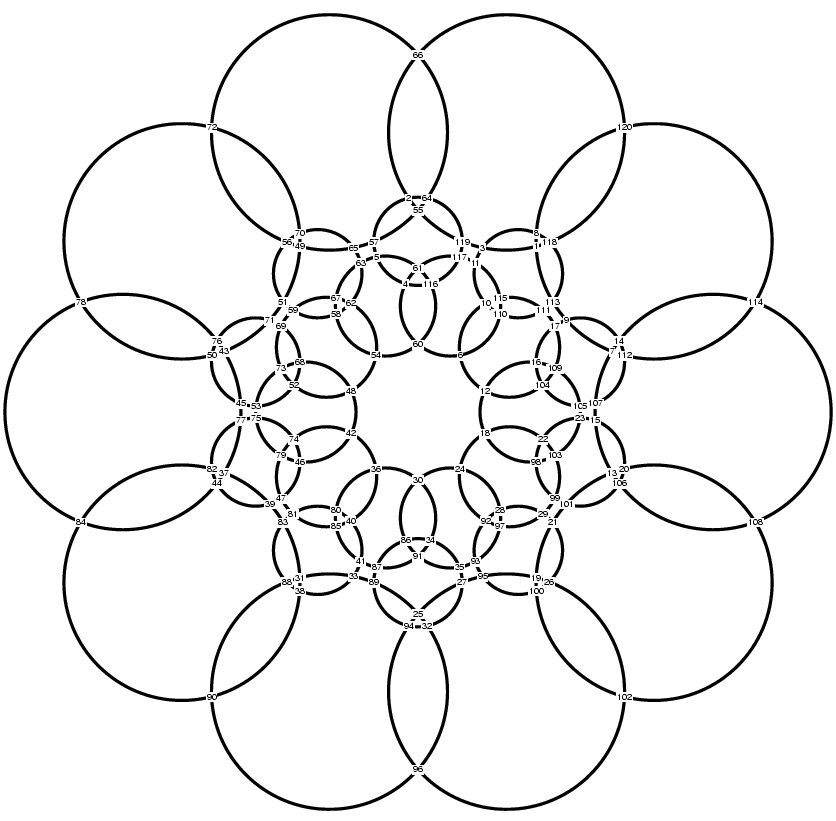
Further layers could be added, but displaying them (with the
small spacing between nodes) would be problematic.
University
of Waterloo | School of Computer Science | 200 University Ave. W. | Waterloo, Ontario Canada | N2L 3G1
| 519.888.4567 | http://www.cgl.uwaterloo.ca/~smann/




