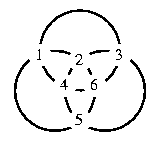
To embed an n x n magic square in a magic circle, we first replicate each circle n times (in our example, n=3):

Now each node in the original magic circle corresponds to an n x n grid of nodes in the new set of circles. At each grid of nodes, we place a copy of our n x n magic circle, except we add to each cell of the magic square the value (k-1)n^2, where k is the value in the original magic circle corresponding to the grid in the new set of circles. In our example, we get:

A few notes are in order. First, the orientation of the magic square on each grid can be arbitrary. Second, the new magic circle will have a sum of SI+(C-I)n^3, where S is the sum of the magic square, C is the sum of the original magic circle, and I is the number of intersections on each circle of the original magic circle. In our example, the sum is 330.
University of Waterloo | School of Computer Science | 200 University Ave. W. | Waterloo, Ontario Canada | N2L 3G1 | 519.888.4567 | http://www.cgl.uwaterloo.ca/~smann/