Proof of non-magic

Last Updated: September 13, 2002

Clifford Pickover gave several sets of circles in his Grand Internet Math Challenge, with the object being to find consecutive integers that make them magic circles. The following is a proof that there is no magic solution using consecutive, positive integers greater than 0 for one of the set of circles in his challenge. The set of rings is the following:

I have colored and labeled these rings to assist in my proof.

The proof starts by showing that there is no assignment of the integers 1,...,28 to the intersection points that results in a set of magic rings. Assume there is such an assignment, and that the sum is k. Consider the red circle. The points labeled A_i and the points labeled B_i must sum to k:

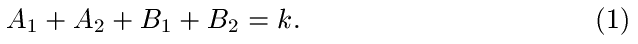
Likewise, if we consider the blue circle and the green circle, we see that

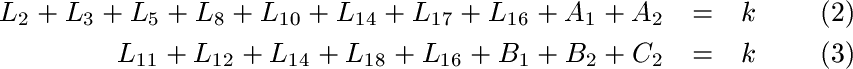
Eliminating k from Equations 1 and 2, and eliminating k from Equations 1 and 3 gives us:

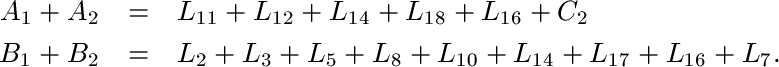
Likewise, a similar derivation shows that

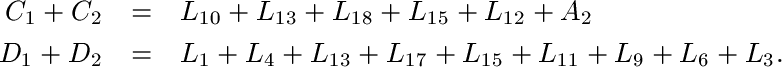
Summing these four equations and keeping only one copy of each L_i on the right gives us the inequality

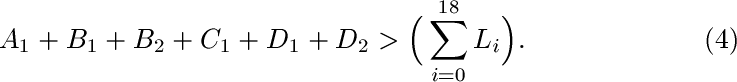
Now, we will maximize the sum of the values on the left-hand size of Equation 4 and minimize the sum of the values on the right-hand side of Equation 4.

To maximize the sum of A₁, B_i, C₁, and D_i, we assign to them the numbers 23,...,28 which have a sum of 153. To minimize the sum of the right hand sides, we assign 1,...,18 to these nodes, giving us

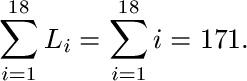
Thus, we see that the maximum of the left-hand-side of Equation 4 is less than the minimum of the right-hand-side of the equation, and hence, no assignment of the integers 1,...,28 to these nodes will result in a magic circle.

From here it is easy to show that no assignment of consecutive integers starting with j>1 will result in a magic circle. Again consider Equation 4, which must hold for any assignment of integers. We know that assigning the integers 1,...,28 will result in the left hand side being strictly less than the right-hand side. If we add j-1 to each integer in such an assignment, the right-hand size increases by 18(j-1) while the left hand side increases by only 6(j-1), and the inequality is worsened.

This proof, of course, says nothing about using a mix of positive and negative integers, nor does it say anything about using non-consecutive integers.
University of Waterloo | School of Computer Science | 200 University Ave. W. | Waterloo, Ontario Canada | N2L 3G1 | 519.888.4567 | http://www.cgl.uwaterloo.ca/~smann/