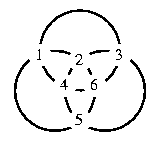Simple Magic Circles
Last Updated: September 12, 2002
Up
In W.S. Andrews's book (Magic Squares and Cubes),
Harry Sayles gives a simple construction for assigning
numbers to get a magic circle. This simple assignment only
applies when the circles meet certain conditions:
- Each pair of circles intersect in either 0 or 2 distinct places;
- no more than 2 circles intersect at one point,
- each circle has the same number of intersections $I$ (which
because of conditions 1 and 2 has to be an even number),
In such a configuration, there will always be an even number of
intersections,
say 2n, where n is the number of pairs of intersecting circles.
The assignment of the numbers 1...2n to the intersection points is
done by first pairing the numbers i to 2n+1-i, and then going through
the n pairs of intersecting circles and arbitrarily assigning one
of the number pairs to the intersection pair (naturally, each pair of
numbers is assigned to one and only one intersection pair).
The result is readily seen to be a magic circle, since each circle
intersects I/2 other circles in a total of I locations, with a sum
of (I/2)(2n+1) as its sum.
The following simple example is easily seen to be a magic circle
of this type:
Other Examples of Simple Magic Circles
Note that "simple" here just refers to the arrangement of
intersections. The configuration itself may look fairly
complex, as seen in the following examples:
University
of Waterloo | School of Computer Science | 200 University Ave. W. | Waterloo, Ontario Canada | N2L 3G1
| 519.888.4567 | http://www.cgl.uwaterloo.ca/~smann/