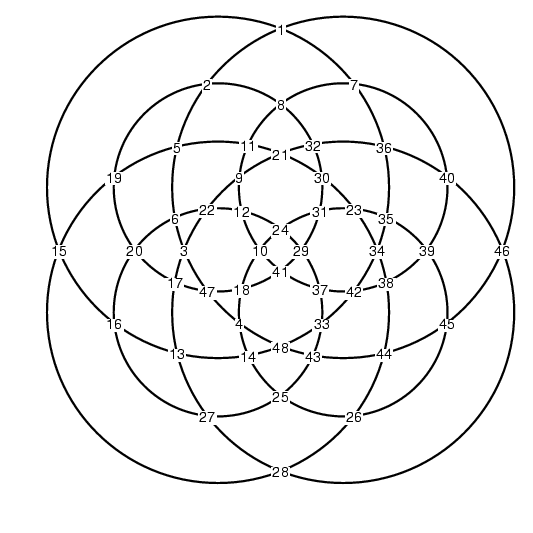

Note that there are eight total circles, each of which intersects six of the other circles in two places, and that exactly two circles meet at each intersection point. Further, there are twelve intersection points on each circle. If we search, we can find four additional circles that pass through eight intersection points:
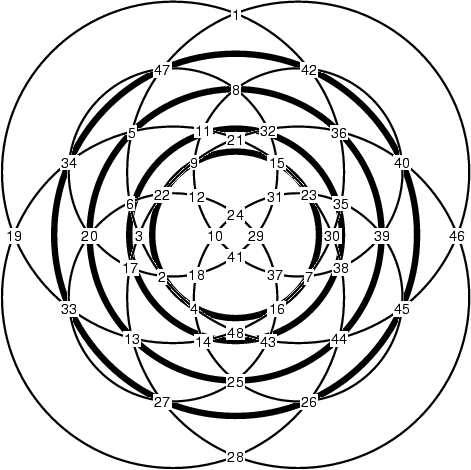
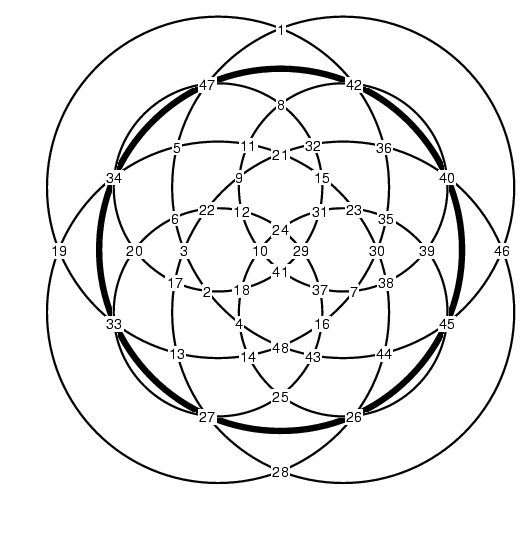
With the numbers available, we have the potential to assign the values 1..48 in such a way as to obtain two more circles that that sum to the magic value of 294. However, looking more closely, you will find that we can not make such an assignment to the middle two of the dark circles above, and if we make such an assignment to either the inner or outer dark circle, then the values at the other circle are forced. Thus, we can assign values to get only one more circle that sums to 294, either the inner dark circle or the outer dark circle. Here's an assignment that makes the outer dark circle sum to 294:
University
of Waterloo | School of Computer Science | 200 University Ave. W. | Waterloo, Ontario Canada | N2L 3G1
| 519.888.4567 | http://www.cgl.uwaterloo.ca/~smann/